二叉树

二叉树是连通无环图，并且每个结点的度最大为2，度就是有几个直接的子结点。

• 二叉树
  • 满二叉树
  • 完全二叉树
  • 平衡二叉树

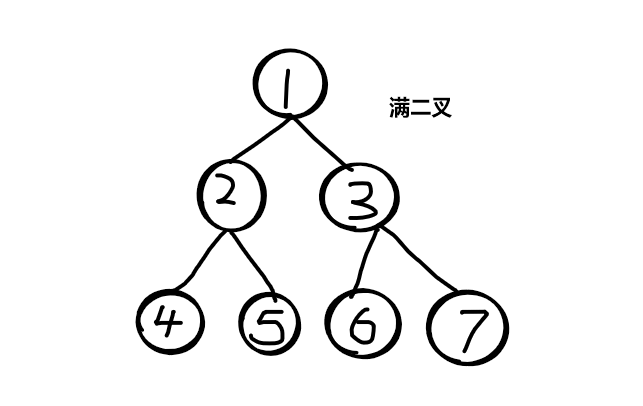
满二叉树

每一层都挂满节点的二叉树，就是满二叉树

节点数：2 ^ h - 1
h 为树的高度（可以理解为二叉树层数）

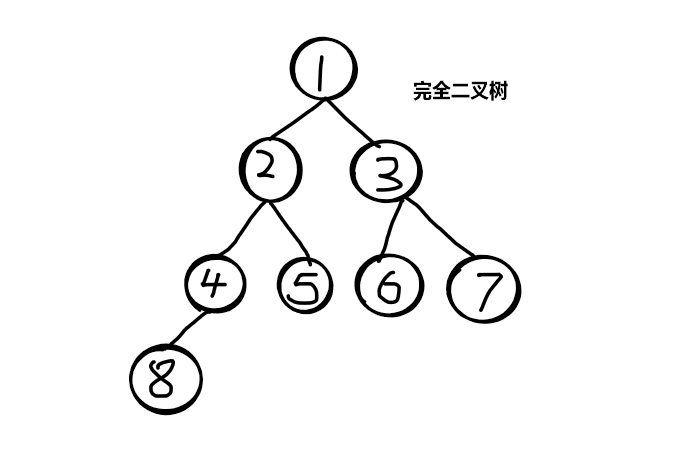
完全二叉树

完全二叉树就是除了最后一层，上层都是满节点，最后一层从左到右排。可以不排满

得出结论满二叉树 “包含” 完全二叉树，反过来不行！

使用场景

二叉树的特点：“叶子节点的位置比较规律”。因此在对数据进行排序或者查找时可以用到它，比如堆排序就使用了它。

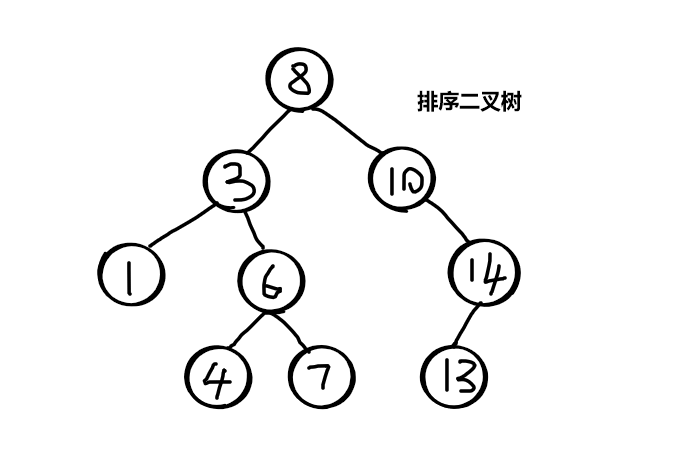
二叉排序树

二叉树的提出其实主要就是为了提高查找效率，比如我们常用的 HashMap 在处理哈希冲突严重时，拉链过长导致查找效率降低，就引入了红黑树

二分查找可以缩短排序的时间，但是它要求 查找的数据必须是有序 的。每次查找、操作时都要维护一个有序的数据集，于是有了二叉排序树这个概念。

• 特点
  • 左子树所有节点值均小于它的根节点的值
  • 右子树所有节点值均大于或等于根节点的值
  • 左、右子树也分别为二叉排序树

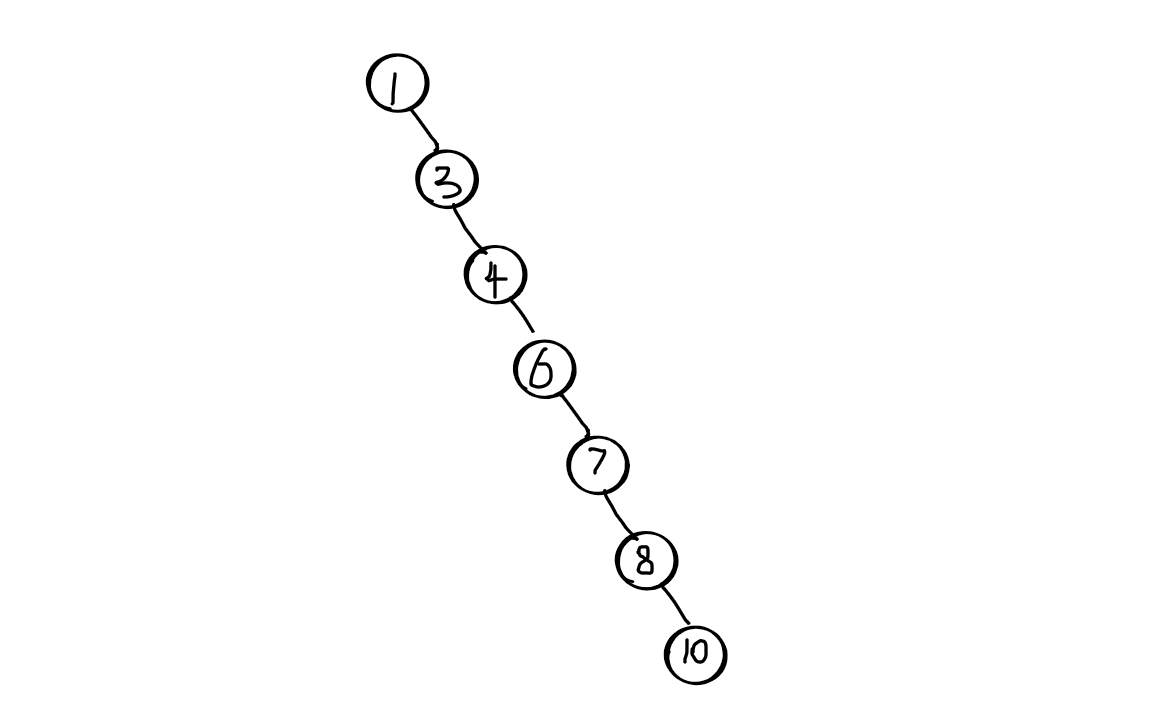
排序二叉树也可能出现下图：

插入的元素是有序的，生成的二叉排序树就是一个链表，这种情况下，需要遍历全部元素才行

插入有序的元素时不太好控制，按二叉排序树的定义，我们无法判断当前的树是否需要调整。

因此就要用到平衡二叉树（AVL 树）了。

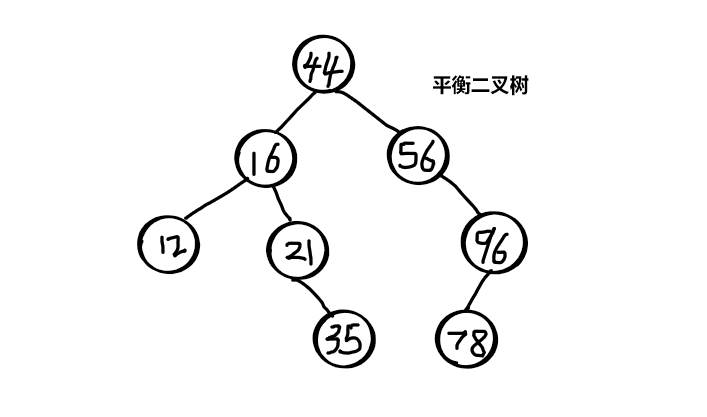
平衡二叉树

平衡二叉树也称为AVI树。平衡二叉树的提出就是为了保证树不至于太倾斜，尽量保证两边平衡。

• 特点
  • 平衡二叉树要么是一棵空树
  • 在AVL树中任何节点的两个子树的高度最大差别为1
  • 子树也必须是一棵AVL树
  • 左子树所有节点都小于根节点的值，右子树节点都大于根节点的值

现有 无序数组 [35,16,44,56,78,12,96,21]

本文通篇都是讲述二叉树概念，未涉及实现，后续补上。