前端向量知识

发表于 2022-07-07 更新于 2023-11-21 分类于可视化

在计算机可视化领域必定少不了向量的运用，本文用来记录向量在可视化领域的基础使用。

向量与标量

向量和标量一样可以进行数学运算。 举个例子，现在有两个向量，v1和 v2，如果让它们相加，其结果相当于将 v1向量的终点（x1, y1），沿着 v2向量的方向移动一段距离，这段距离等于 v2向量的长度。这样，我们就可以在平面上得到一个新的点（x1 + x2, y1 + y2），一条新的线段[(0, 0), (x1 + x2, y1 + y2)]，以及一段折线：[(0, 0), (x1, y1) , (x1 + x2, y1 + y2)]。

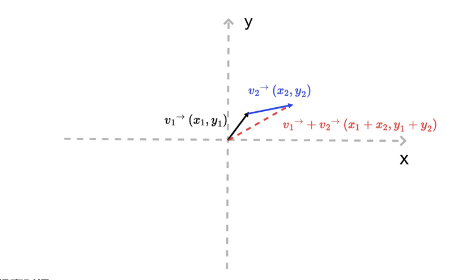
而红色向量则是$v_1 + v_2$的结果。

一个向量包含长度和方向信息

向量长度可以用x、y的平方和的平方根来表示，用JS代码表示就是：

1
2
3

v.length = function() {
    return Math.hypot(this.x, this.y)
};

方向则可以用v与x轴的夹角来表示：

1
2
3

v.dir = function() {
    return Math.atan2(this.y, this.x);
}

根据上面已有公式，可以退出向量v的值：
向量v在x轴的长度 = 已知向量长度 * 横方向长度 = 向量长度 * 已知向量与横方向的余弦值，y轴长度类似，既：

1 2	v.x = v.length * Math.cos(v.dir); v.y = v.length * Math.sin(v.dir);

这个推论意味着一个重要的事实：我们可以很简单地构造出一个绘图向量。也就是说，如果我们希望以点 ($x_0, y_0$) 为起点，沿着某个方向画一段长度为 length 的线段，我们只需要构造出如下的一个向量就可以了。

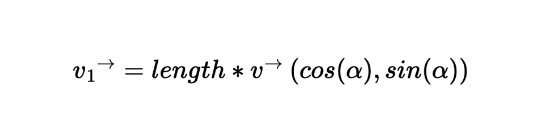
这里的α是与 x 轴的夹角，v 是一个单位向量，它的长度为 1。然后我们把向量 (x0, y0) 与这个向量 v1相加，得到的就是这条线段的终点。

向量的点乘

在 N 维线性空间中，a、b 向量点积的几何含义，是 a 向量乘以 b 向量在 a 向量上的投影分量。它的物理含义相当于 a 力作用于物体，产生 b 位移所做的功。点积公式如下图所示：

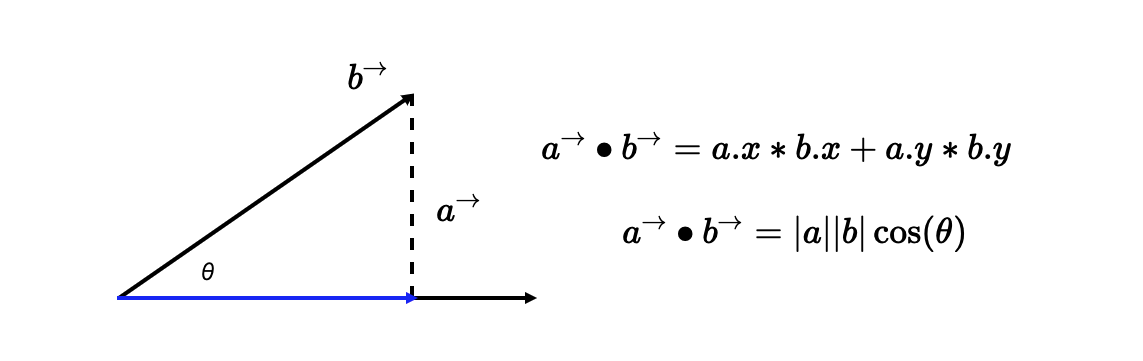
证明过程:

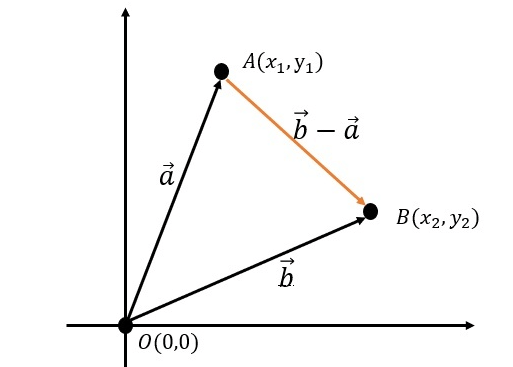
设 $\overrightarrow{a}$ = (x$_1$, y$_1$) , $\overrightarrow{b}$ = (x$_2$, y$_2$)，则 $\overrightarrow{b}$ - $\overrightarrow{a}$ = (x$_2$ - x$_1$, y$_2$ - y$_1$)

在▲$ABC$中，根据余弦定理有：
$AB^2=OA^2+OB^2-2OA\cdot OB \cdot cos∠AOB$，

$|\overrightarrow{b}-\overrightarrow{a}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 2|\overrightarrow{a}||\overrightarrow{b}|cos\theta$，其中$\theta = ∠AOB$

根据向量模运算：
$(x_2-x_1)^2+(y_2-y_1)^2 = x_1^2 + y_1^2 + x_2^2 + y_2^2 - 2|\overrightarrow{a}||\overrightarrow{b}|cos\theta$

最后开平方简化后的终极结果是：
$x_1x_2 + y_1y_2 = |\overrightarrow{a}||\overrightarrow{b}|cos\theta$

点乘的几何意义

$\overrightarrow{ a } \cdot \overrightarrow{b}$ > 0 则方向基本相同，呈锐角，夹角在0$^\circ$到90$^\circ$。
$\overrightarrow{ a } \cdot \overrightarrow{b}$ = 0 则正交，相互垂直。
$\overrightarrow{a} \cdot \overrightarrow{b}$ < 0 则方向相反，呈钝角或平角，夹角在90$^\circ$到180$^\circ$。
$\overrightarrow{a} \cdot \overrightarrow{b}$ = |$\overrightarrow{a}$| |$\overrightarrow{b}$|，则两个向量平行，夹角为0$^\circ$。

向量的叉乘

叉乘和点乘有两点不同：首先，向量叉乘运算的结果不是标量，而是一个向量；其次，两个向量的叉积与两个向量组成的坐标平面垂直。怎么理解呢？我们接着往下看。

以二维空间为例，向量 a 和 b 的叉积，就相当于向量 a（蓝色带箭头线段）与向量 b 沿垂直方向的投影（红色带箭头线段）的乘积。那如下图所示，二维向量叉积的几何意义就是向量 a、b 组成的平行四边形的面积。

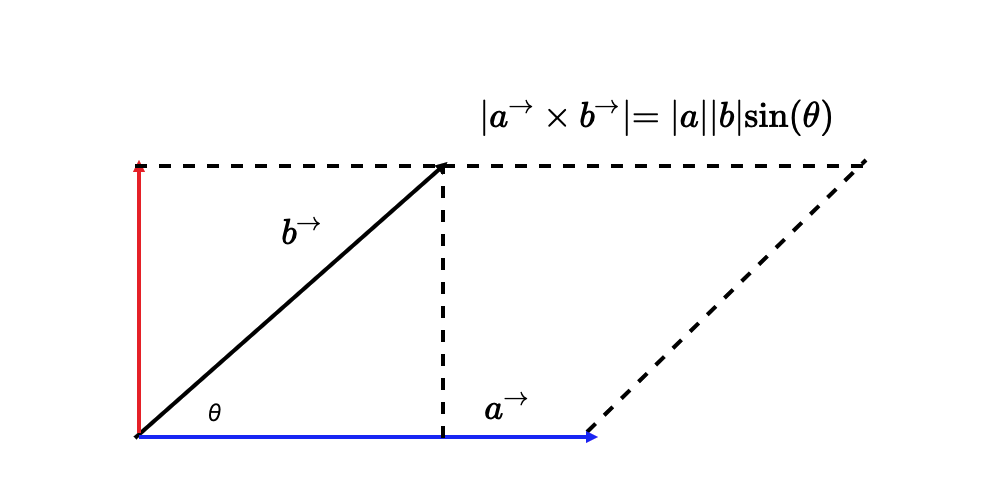
叉乘的几何意义

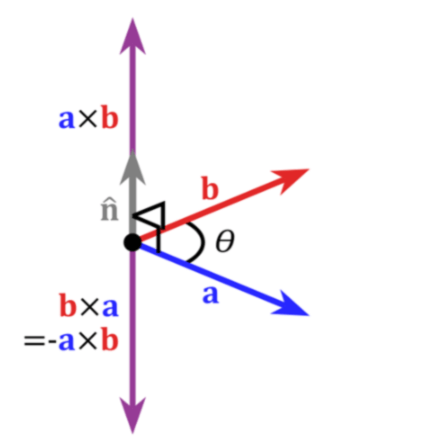
在3D图形学中，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。如下图所示：

那叉乘在数学上该怎么计算呢？假设，现在有两个三维向量 a(x1, y1, z1) 和 b(x2, y2, z2)，那么，a 与 b 的叉积可以表示为一个如下图的行列式：

$a × b = \begin{Bmatrix} i&j&k\\ x_1&y_1&z_1\\ x_1&y_2&z_2\\ \end{Bmatrix}$

其中 i、j、k 分别是 x、y、z 轴的单位向量。我们把这个行列式展开，就能得到如下公式：

1	a X b = [y1 * z2 - y2 * z1, -(x1 * z2 - x2 * z1), x1 * y2 - x2 * y1]

我们计算这个公式，得到的值还是一个三维向量，它的方向垂直于 a、b 所在平面。我们使用右手法则确定其方向。

$The\,End$

相关概念